post 10

10 subscribers! woohoo! I’ve probably mentioned this project to only 30 people. There’s no rush to make it popular.

This is the first of about 5 short articles on gears.
If you like reading, there's a backstory at the end.

So what is it?

This is an intergalactic planetary gear set.

What is it good for?
Wikipedia covers it well in the relevant section. (unlike some of the other sections, notes in the backstory)

Let's play with some configurations

I highly recommend this simple online simulator.

Planetary Gear Simulator

This is a great way to get an understanding of the basics and constraints when dimensioning the gears.

Further down in this post are some links for making proper designs. For now, we will start with a simple example and a few diagrams.

Making diagrams

An easy way to work with planetary gear sets is to consider their cross-section.

In this case, we add a center shaft and an external brake. In a moment we will connect these to parts of the gear set in order to achieve some functionality.

I’ve also faded out the bottom half of the design. Once you understand what you are looking at, it becomes unnecessary to keep drawing everything in twice.

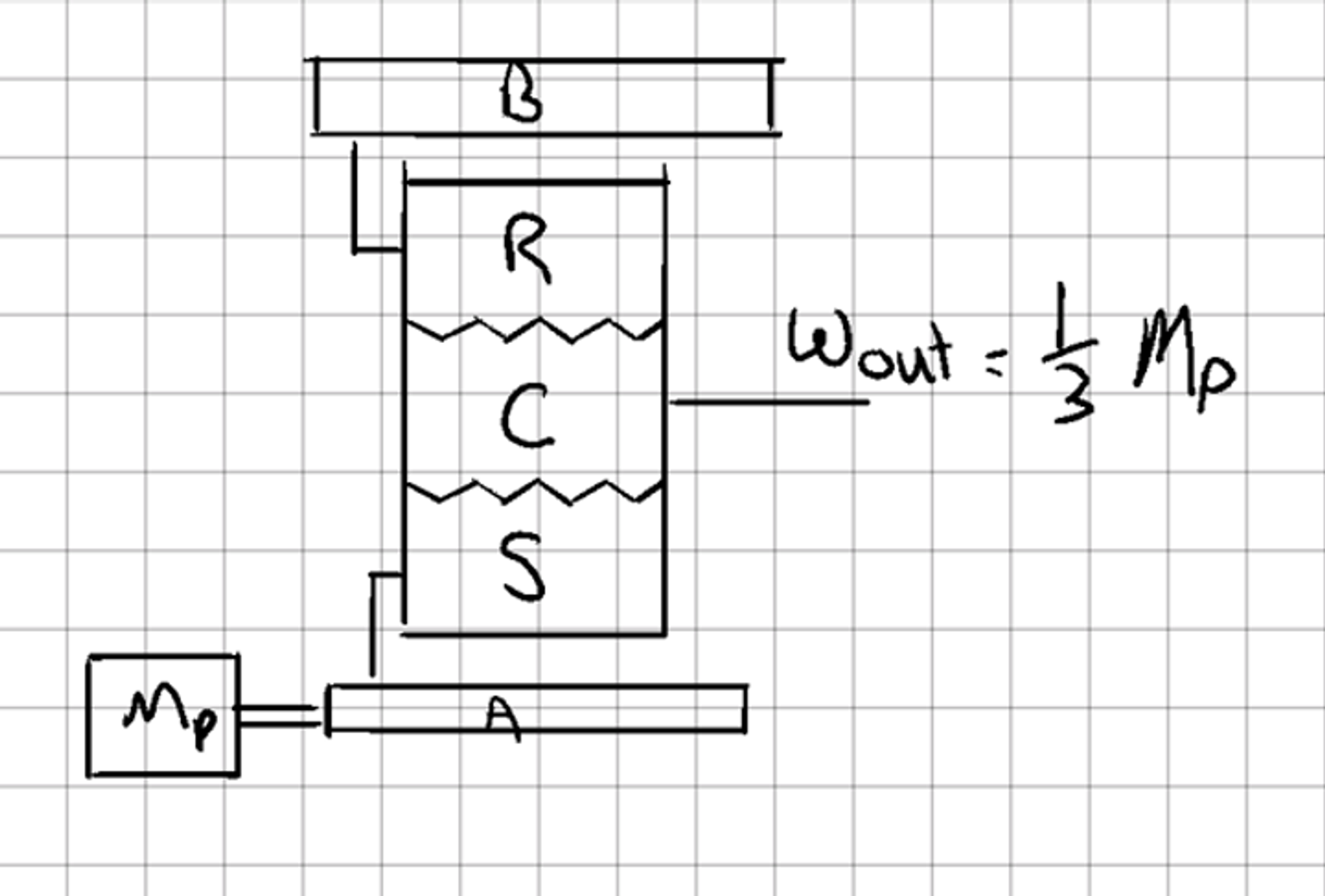
An example as simple as 1+2=3

To make things as simple as possible, we’ll start with this beautiful arrangement.

Fixed ring mode

Here the Sun has 32 teeth and the Ring has 64 teeth. If you put this into the simulator, you will find that the planets will have 16 teeth.

Now if we hold the ring gear fixed and turn the sun gear, we will find that the carrier will move at 1/3rd the speed of the Sun gear.

Here it is as a diagram.

Let's now do the math to work out how we got to this.

The Wikipedia article on Epicyclic gearing is rather difficult to follow. Equations everywhere. But, most of the time, we can get by with just this one:

$$ N_s w_s+N_r w_r=(N_s+N_r)w_c $$

Where

• Ns and Nr means “number of teeth” of the sun and ring gears
• Ws, Wr, Wc means the speed of the sun, the ring and the Carrier

The most important takeaway of all is:

The Carrier doesn’t have any teeth itself, but it effectively has the same number of teeth as the Sun + the Ring.

(There is a link to a YouTube later that explains why)

Now, if we plug in our number of teeth from before:

$$ N_{s} w_{s}+N_{r}w_{r}=(N_{s}+N_{r})w_{c} \\ 32 w_{s}+64w_{r}=(32+64)w_{c}\\or\\ 1w_{s}+2w_{r}=3w_{c} $$

Or, one can simply think of it as “1+2=3”.

Now that we have this simple equation, we can prove that it works by setting the speed of the ring to zero:

$$ \left\{\begin{matrix} 1w_s+2w_r=3w_c\\ w_s=w_{in}\\ w_r=0\\ w_c=w_{out}\\ \end{matrix}\right.\\ 1w_{in} + 2(0) = 3w_{out}\\ w_{out} = (1/3) w_{in} $$

That’s it: If you hold the ring fixed, the carrier turns 3x slower than the Sun.

Now, let's look at a few other scenarios or modes.

Fixed sun mode

It’s pretty much the same process.

$$ \left\{\begin{matrix} 1w_s+2w_r=3w_c\\ w_s=0\\ w_r=w_{in}\\ w_c=w_{out}\\ \end{matrix}\right.\\ 1(0)+2w_{in} = 3w_{out}\\ w_{out} =(2/3) w_{in} $$

Fixed carrier mode

Now we lock the carrier

You’ve probably also noticed by now that the fraction above the arrow matches the numbers on the gears. So, you pretty much get the ratio straight from the diagram. Here's the math in any case.

$$ \left\{\begin{matrix} 1w_s+2w_r=3w_c\\ w_s=w_{in}\\ w_r=w_{out}\\ w_c=0\\ \end{matrix}\right.\\ 1w_{in}+2w_{out} = 3(0)\\ w_{out} = (-1/2) w_{in} $$

Locked mode

When we lock two parts of the system togher.

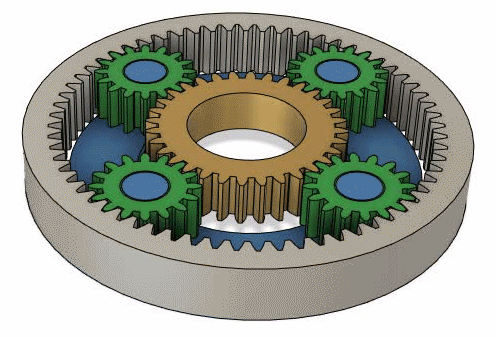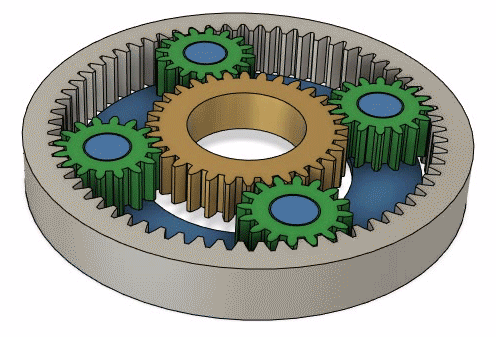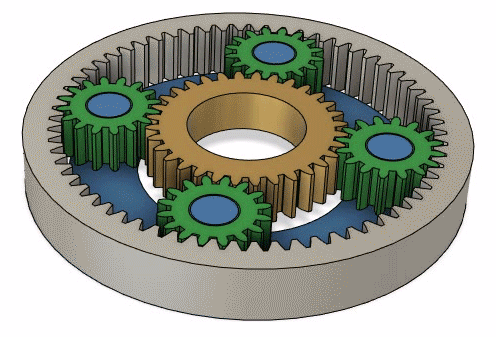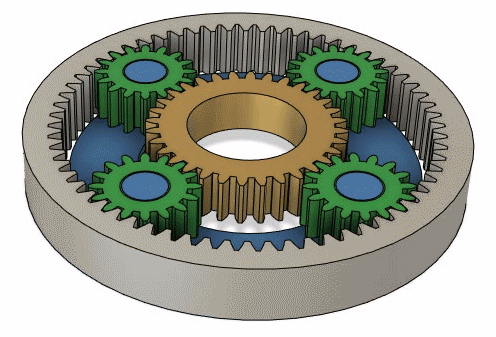
And now the equation.

$$ \left\{\begin{matrix} 1w_s+2w_r=3w_c\\ w_s=w_{in}\\ w_r=w_{in}\\ w_c=w_{out}\\ \end{matrix}\right.\\ 1w_{in}+2w_{in} = 3w_{out}\\ 3w_{in}= 3w_{out}\\ w_{out} = w_{in} $$

This works regardless of which parts are locked together.

Neutral mode

Finally, we look at the case when one of the parts is not connected to anything.

In this case, it looks like there should be some connection between the input and output.

Let’s look at the Math:

$$ \left\{\begin{matrix} 1w_s+2w_r=3w_c\\ w_s=w_{in}\\ w_r=?\\ w_c=w_{out}\\ \end{matrix}\right.\\ 1w_{in}+2(?) = 3w_{out}\\ w_{out} = (1/3)w_{in} + (2/3)? $$

There is no clear answer for the speed.

What we are really looking at here is a form of Neutral. This will become important in the next post when we look at compound gearboxes.

In simulations, what often happens is that the output follows the input at 1:1. But, in reality, it is more likely that any small load on the output will result in both the input and output driving the gear which is free to move. The result in this case is:

$$ w_r = (3/2)w_{out} - (1/2)w_{in} $$

Of course, it won’t be a perfect neutral. If you don’t have any load on the output, any small amount of friction in the gearbox is going to cause some of the input to appear at the output.

On gear ratios, speed and torque.

In the last examples, we looked at cases where we have one known input speed and achieve one output speed. In all these cases, the equation reduces down to something that looks a lot like:

$$ gearsize_{in}\times speed_{in} = gearsize_{out}\times speed_{out} $$

Which is pretty much the equation for standard gear ratios.
If this is the case, then one can also calculate the torque. This post is a little long for an explanation, so here it is in Lego:

In short: If your output gear is 3 times bigger than the input, it will turn 3 times slower and have 3 times the torque… (losses, friction, something, something )

How to seriously design a gear set

This is quite useful. They even have a simulator, but I haven’t tried it as yet.

Planetary Gears

Planetary geartrain design for spur and helical gears.

Drivetrain HubChad Glinsky

How do derive these equations?

If you're left with any questions: This video is a good start.

How to model a gearset

I made the example model on Fusion 360 following this tutorial.
It covers some of the math as well.

I used the Fusion 360 animation tool to make videos, then a video editor to process them into Gifs. Because Fusion 360 can't animate joints, it was a little tedious to rotate all the parts for the animation. But not too difficult once I gave it some thought.

Drawing the diagrams.

The method of drawing the diagrams was originally inspired by this video. Which may well be easier to follow now that you have learned the basics.

To teach myself, I drew many sketches of gear sets. Here is one example. I actually prefer this aesthetic to the final schematics.

The final schematics are made in Inkscape. Which is a free version of Adobe Illustrator. All the schematics can be downloaded from Wiki Commons and edited to make your own designs.

While researching schematics, I reached out to Wiki user Jahobr who has the animated gifs on the Wikipage.
Amoungst his works, I found this way to describe the gearsets.

He said “The style is sometimes used in literature” and linked me to some other diagrams he put together

I also found this one googling around.

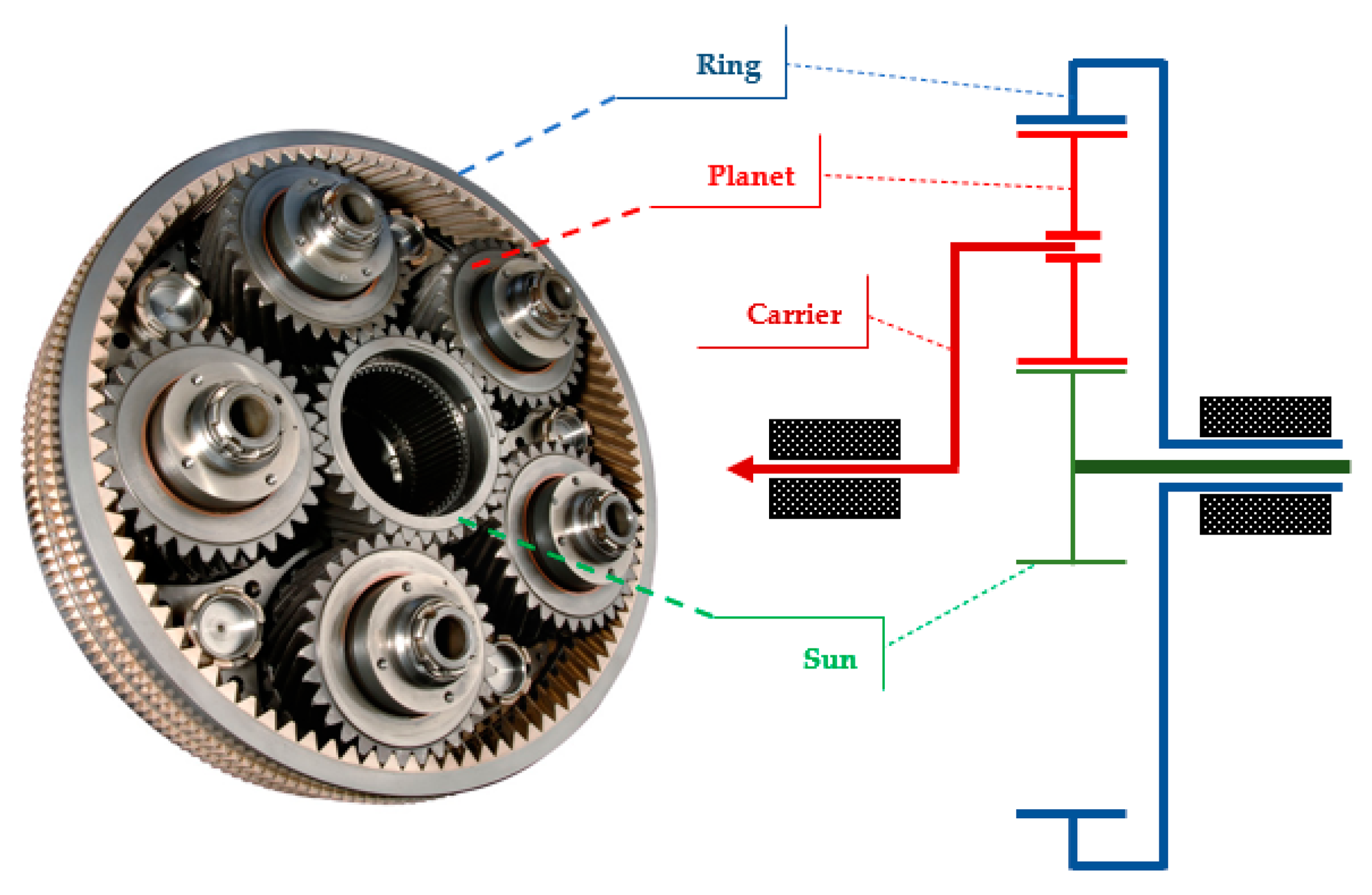
I guess this common literature way works just as well.

Backstory

Until yesterday, I had this section at the top of this post. Then, after looking up a recipe for toast and thinking "Dude, nobody gives a shit about how your precious grand-mama loaded her toaster", I decided that this will be a recipe-first blog.

Also, I said I wouldn’t do this at all.

However, I have some concept work coming up which requires some basic understanding of a few things. These gear sets are one of those things. They are not all that complicated, but they can be confusing. So, I’m laying down this post as a building block, or an anchor point to refer back to.

Normally, one would just link the Wikipedia article. However, currently (2024), that page makes me feel like this:

I suppose it’s hard to make Wiki pages for stuff like this. The scope can get intense pretty quickly. And it might be impossible to cater for the wide range of audiences and their applications. Maybe this is written in a useful way for someone.

Moving on.

Here are some of my notes and tools that I’ve collected to stay sane.

This clunky little post is probably not a good read either. It might be helpful if you have reached this page because you have some applications that you are trying to understand better.

And It’s not like we’re trying to sell them to you here.

Anyway, this is a post on Planetary gear sets
Or “Epicyclic gearing”, said nobody, ever.

on licensing some content

Since I complained about the Wikipedia article, I decided to contribute a little by releasing these animations on Creative Commons. They are currently on the articles discussion page in case an experienced editor would like to make the page better. I'll probably write to one of the original contributors about it first.

This would also be the first time I've shared anything public about this project.

Anyway, this is what the CC0 link means on the images and animations. It also has a good feeling of productivity. This work is leading towards some concepts that I think are novel. However, those concepts might also turn out to be useless. In that case, at least some of the pre-work is not wasted by being available in the public domain.

Update

20240205

This post didn’t originally have the schematic diagrams or the Neutral case in it. As I put together the subsequent posts, I'm coming back to this one to fill it out.

Finally, I originally had the Creative Commons licenses to CC-BY-4.0, but now updated it all to CC0. The philosophy here is that people will either credit your work, or they won’t. A license is not likely to change that. However, a CC0 makes it very easy for people who “want/need” to credit you since they don’t really need to think twice about getting it right. I mentioned talking to the Wiki user Jahobr . While searching around, I found his work referenced on the JPL website.

I figure that is infinitely cooler than trying to argue about BY clause against some generated website that copies all your content and jams a lot of spam in between the text to generate passive income. Hopefully, you're not reading this there. If you are, the original article was on robot company ddot net. I don't even want to know.

Next.

In the next post, there will be a little work on chaining these gear sets together to form “compound planetary gear sets”